With the growing popularity of hybrid quantum-classical algorithms as a way of potentially achieving a quantum advantage on Noisy Intermediate-Scale Quantum (NISQ) devices, there were a number of talks on this topic at this year’s QIP conference in Boulder, Colorado. One of the talks that I found the most interesting was given by John Napp from MIT on how “Low-depth gradient measurements can improve convergence in variational hybrid quantum-classical algorithms” based on work done with Aram Harrow (https://arxiv.org/abs/1901.05374).
What are variational hybrid quantum-classical algorithms?
They are a class of optimisation algorithms in which the quantum and classical computer work closely together. Most variational algorithms follow a simple structure:
- Prepare a parameterised quantum state
which can take the form
where the
are Hermitian operators. The type of parameters and operators depend on the device that is being targeted and
is an easy-to-prepare initial state.
- Carry out measurements to determine information about the classical objective function
you wish to minimise (or maximise) where
and
is some Hermitian observable (for example corresponding to a physical Hamiltonian). Due to the randomness of quantum measurements, many preparations and measurements of
are required to obtain a good estimate of
.
- Use a classical optimisation method to determine a new value for
that will minimise
. This is a stochastic optimisation problem since we do not have direct access to
– only noisy access through measurements.
- Repeat steps 1-3 until the optimiser converges.
Examples of this type of algorithm are the variational quantum eigensolver (VQE) used to calculate ground states of Hamiltonians and the quantum approximate optimisation algorithm (QAOA) for combinatoric optimisation problems.
Gradient measurements
To obtain information about the objective function , it can be expressed in terms of easily measurable operators:
where are tensor products of Pauli operators. Then to carry out the optimisation, derivative-free methods such as Nelder-Mead can be used. However, if one wishes to use derivative-based methods such as BFGS or the conjugate gradient method, we need an estimate of the gradient
. A numerical way to do this is by finite-differencing which only requires measurements of
, for small
,
where is the unit vector along the
component. Each time
is evaluated with different parameters, which can be done in low-depth, many repeat measurements are required.
An alternative method is to take measurements that correspond directly to estimating the gradient . This is referred to as an analytic gradient measurement and usually only requires a slightly greater circuit depth than measuring the objective function. Previously it was not clear whether these analytic gradient measurements could offer an improvement over schemes that used finite-differences or derivative-free methods, but as we will see, Harrow and Napp have proved in this paper that in some cases it can substantially improve convergence rates.
For the rest of this post, the term zeroth-order will refer to taking measurements corresponding to the objective function. First-order will refer to algorithms which make an analytic gradient measurement (and this can generalise to kth-order where the kth derivatives are measured). It is clear how zeroth-order measurements are made – by measuring the Pauli operators with respect to the state
. But how do we make first-order measurements corresponding to the gradient?
The state can be rewritten as
where the unitary
and for
the sequence
is defined as
. Therefore,
. This can be differentiated via the chain rule to find:
Recalling that and writing the Pauli decomposition of
as
where
are products of Pauli operators, the derivative can be rewritten as
This can then be estimated using a general Hadamard test which is used to estimate real (or imaginary) parts of expected values. The circuit that yields an unbiased estimator for is:
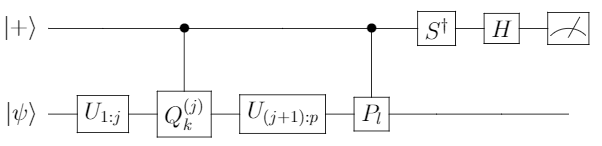
Measuring every term in the expansion is unnecessary to estimate or its derivatives. So for all orders, a further sampling step is carried out, where terms in the expansion are sampled from (using a strategy where terms with smaller norms are sampled from with smaller probability) and measured to determine a specific unbiased estimator, but I will not go into details here.
Black-box formulation
To quantify how complex an optimisation problem is, the function to be optimised can be encoded in an oracle. The query complexity of the optimisation algorithm can then be defined as the number of calls made to the oracle. This black-box formalism is typically used in the study of classical convex optimisation, here the quantum part of the variational algorithm has been placed into the black box.
In this black-box model, the classical optimisation loop is given an oracle encoding
. The optimiser is not given specifics about the problem, but it could be promised that the objective function will have certain properties. The outer loop queries
with a state parameterisation
, parameters
and a set
containing integers
. The black box then prepares the state
and if
performs a zeroth-order measurement estimating
. Otherwise a kth-order query is performed to estimate the derivative of
with respect to
. The query cost of this model is the number of Pauli operators measured.
How many measurements are sufficient to converge to a local minimum?
Imagine now that we restrict to a convex region of the parameter space on which the objective function is also convex. We would like to know the upper bounds for the query complexity when optimising to precision
, or in other words how many measurements are required so that convergence to the minimum is guaranteed.
In the paper, results from classical convex optimisation theory are used to compare a zeroth-order algorithm with stochastic gradient descent (SGD) and stochastic mirror descent (SMD, a generalisation of SGD to non-Euclidean spaces). For convex and -strongly convex functions, the upper bounds are shown to be:
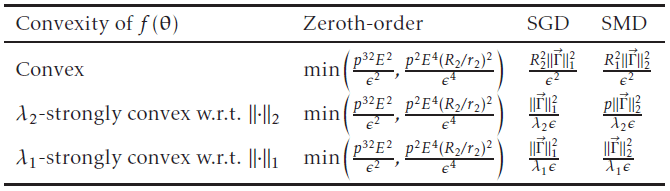
Here and
are parameters related to the Pauli expansion of
and
are balls in the convex region we are optimising over. It is clear that SGD and SMD will typically require less measurements to converge to the minimum compared to zeroth-order, but whether SGD outperforms SMD (or vice versa) depends on the problem at hand.
It is important to note that these are the best theoretical bounds, for some derivative-free algorithms (such as those based on trust regions) it can be hard to prove good upper bounds and guarantees of convergence. However they can perform very well in practice and so zeroth-order could still potentially outperform SGD and SMD.
Can first-order improve over zeroth-order measurements?
To answer this question, a toy problem was studied. Consider a class of 1-local -qubit Hamiltonians defined as the set
where
and
These are perturbations about
where
is the strength and
the direction of the perturbation. We wish to know how many measurements are needed to reach the ground state of
. This problem is trivial (the lowest eigenvalue and it’s associated eigenvector can be written down directly) which is why the black-box formulation is necessary to hide the problem. The resulting upper and lower query complexity bounds for optimising the family
is found to be:

The proof of the lower bound is too complicated to explain here. Proving the upper bound, in particular for first-order, is simpler and relies on using a good parameterisation
in our optimisation algorithm. is a natural choice for the family
as each qubit is polarised in the
plane. The corresponding objective function is then
which is strongly convex near the optimum and so stochastic gradient descent performs well here. Note that making higher-order queries is unnecessary in this case as the optimal bounds can be achieved with just first-order.
Conclusion
Ultimately Harrow and Napp have shown that there are cases in which taking analytic gradient measurements in variational algorithms for use in stochastic gradient/mirror descent optimisation routines (compared to derivative-free methods) could help with convergence. It would be interesting to see what happens with more complicated problems and if more general kth-order measurements will provide benefits over first-order. Another extension that is mentioned in the paper is to see what the impact of noisy qubits and gates is on the convergence of the optimisation problem.
I personally am most eager to see how these results will hold up in practice. For example, it would be interesting to see a simple simulation performed for the toy problem comparing zeroth-order optimisers with those that take advantage of analytic gradient measurements.
