One of the most famous models for quantum computation is the black-box model, in which one is given a black-box called oracle encoding a unitary operation. With this oracle one can probe the bits of an unknown bit string 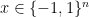 (the paper uses the set
(the paper uses the set 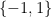 instead of
instead of 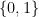 , which I will keep here) . The main aim of the model is to use the oracle to learn some property given by a Boolean function
, which I will keep here) . The main aim of the model is to use the oracle to learn some property given by a Boolean function 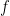 of the bit string
of the bit string  , for example, its parity. One use of the oracle is usually referred as a query, and the number of queries a certain algorithm performs reflects its efficiency. Quite obviously, we want to minimize the number of queries. In more precise words, the bounded-error quantum query complexity of a Boolean function
, for example, its parity. One use of the oracle is usually referred as a query, and the number of queries a certain algorithm performs reflects its efficiency. Quite obviously, we want to minimize the number of queries. In more precise words, the bounded-error quantum query complexity of a Boolean function 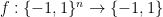 is denoted by
is denoted by 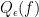 and refers to the minimum number of queries a quantum algorithm must make on the worst-case input x in order to compute
and refers to the minimum number of queries a quantum algorithm must make on the worst-case input x in order to compute  with probability
with probability  .
.
Looking at the model and the definition for the quantum query complexity, one might ask “but how can we find the query complexity of a certain function? Is there an easy way to do so?”. As usual in this kind of problem, finding the optimal performance of an algorithm for a certain problem or an useful lower bound for it is easier said than done. Nonetheless, there are some methods for tackling the problem of determining 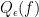 . There are two main methods for proving lower bounds, known as the polynomial method and the adversary method. In this post we shall talk about the first, the polynomial method, and how it was improved in the work of Arunachalam et al.
. There are two main methods for proving lower bounds, known as the polynomial method and the adversary method. In this post we shall talk about the first, the polynomial method, and how it was improved in the work of Arunachalam et al.
The polynomial method
The polynomial method is a lower bound method based on a connection between quantum query algorithms and, as the name suggests, polynomials. The connection comes from the fact that for every t-query quantum algorithm 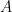 that returns a random sign
that returns a random sign  (i.e.
(i.e. 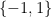 ) on input
) on input  , there exists a degree–
, there exists a degree–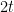 polynomial
polynomial  such that
such that 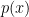 equals the expected value of
equals the expected value of  . From this it follows that if
. From this it follows that if 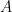 computes a Boolean function
computes a Boolean function 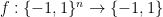 with probability at least
with probability at least  , then the polynomial
, then the polynomial  satisfies
satisfies  for every
for every  (the factor of
(the factor of 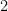 comes from the image being
comes from the image being 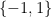 instead of
instead of 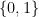 ). Therefore we can see that the minimum degree of a polynomial
). Therefore we can see that the minimum degree of a polynomial  that satisfies
that satisfies  for every
for every  , called the approximate (polynomial) degree and denoted by
, called the approximate (polynomial) degree and denoted by 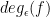 , serves as a lower bound for the query complexity
, serves as a lower bound for the query complexity 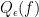 . Hence the problem of finding a lower bound for the query complexity is converted into the problem of lower bounding the degree of such polynomials.
. Hence the problem of finding a lower bound for the query complexity is converted into the problem of lower bounding the degree of such polynomials.
Converse to the polynomial method
We now have a method for proving lower bounds for quantum query algorithms by using polynomials. A natural question that can arise is whether the polynomial method has a converse, that is, if a degree-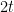 polynomial leads to a
polynomial leads to a 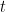 –query quantum algorithm. This would in turn imply a sufficient characterization of quantum query algorithms. Unfortunately, Ambainis showed in 2006 that this is not the case, by proving that for infinitely many
–query quantum algorithm. This would in turn imply a sufficient characterization of quantum query algorithms. Unfortunately, Ambainis showed in 2006 that this is not the case, by proving that for infinitely many  , there is a function
, there is a function 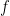 with
with 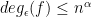 and
and 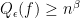 for some positive constants
for some positive constants  . Hence the approximate degree is not such a precise measure for quantum query complexity in most cases.
. Hence the approximate degree is not such a precise measure for quantum query complexity in most cases.
In the view of these negative results, the question that stays is, is there some refinement to the approximate polynomial that approximates 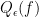 up to a constant factor? Aaronson et al. tried to answer this question around 2016 by introducing a refined degree measure, called block-multilinear approximate polynomial degree and denoted by
up to a constant factor? Aaronson et al. tried to answer this question around 2016 by introducing a refined degree measure, called block-multilinear approximate polynomial degree and denoted by 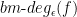 , which comes from polynomials with a so-called block-multilinear structure. This refined degree lies between
, which comes from polynomials with a so-called block-multilinear structure. This refined degree lies between 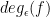 and
and  , which leads to the question of how well that approximates
, which leads to the question of how well that approximates 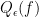 . Once again, it was later shown that for infinitely many
. Once again, it was later shown that for infinitely many  , there is a function
, there is a function 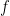 with
with 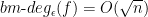 and
and  , ruling out the converse for the polynomial method based on the degree
, ruling out the converse for the polynomial method based on the degree 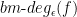 and leaving the question open until now, when it was answered by Arunachalam et al., who gave a new notion of polynomial degree that tightly characterizes quantum query complexity.
and leaving the question open until now, when it was answered by Arunachalam et al., who gave a new notion of polynomial degree that tightly characterizes quantum query complexity.
Characterization of quantum algorithms
In few words, it turns out that 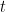 -query quantum algorithms can be fully characterized using the polynomial method if we restrict the set of degree-
-query quantum algorithms can be fully characterized using the polynomial method if we restrict the set of degree-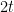 polynomials to forms that are completely bounded. A form is a homogeneous polynomial, that is, a polynomial whose non-zero terms all have the same degree, e.g.
polynomials to forms that are completely bounded. A form is a homogeneous polynomial, that is, a polynomial whose non-zero terms all have the same degree, e.g.  is a form of degree
is a form of degree 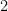 . And the notion of completely bounded involves the idea of a very specific norm, the completely bounded norm (denoted by
. And the notion of completely bounded involves the idea of a very specific norm, the completely bounded norm (denoted by  ), which was originally introduced in the general context of tensor products of operator spaces. But before we venture ourselves into this norm, which involves symmetric tensors and other norms, let us state the main result of the quantum query algorithms characterization.
), which was originally introduced in the general context of tensor products of operator spaces. But before we venture ourselves into this norm, which involves symmetric tensors and other norms, let us state the main result of the quantum query algorithms characterization.
Let ![\beta: \{-1,1\}^n \to [-1,1] \beta: \{-1,1\}^n \to [-1,1]](https://s0.wp.com/latex.php?latex=%5Cbeta%3A+%5C%7B-1%2C1%5C%7D%5En+%5Cto+%5B-1%2C1%5D&bg=ffffff&fg=000000&s=0) and
and 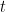 a positive integer. Then, the following are equivalent.
a positive integer. Then, the following are equivalent.
1. There exists a form  of degree
of degree 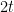 such that
such that 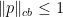 and
and 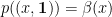 for every
for every  , where
, where 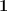 is the all-ones vector.
is the all-ones vector.
2. There exists a 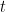 -query quantum algorithm that returns a random sign with expected value
-query quantum algorithm that returns a random sign with expected value 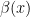 on input
on input  .
.
In short, if we find a form of degree 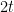 which is completely bounded (
which is completely bounded (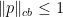 ) and approximates a function
) and approximates a function 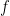 that we are trying to solve, then there is a quantum algorithm which makes
that we are trying to solve, then there is a quantum algorithm which makes 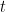 queries and solves the function. Hence we have a characterization of quantum algorithms in terms of forms that are completely bounded. But we still haven’t talked about the norm itself, which we should do now. It will involve a lot of definitions, some extra norms and a bit of C*-algebra, but fear not, we will go slowly.
queries and solves the function. Hence we have a characterization of quantum algorithms in terms of forms that are completely bounded. But we still haven’t talked about the norm itself, which we should do now. It will involve a lot of definitions, some extra norms and a bit of C*-algebra, but fear not, we will go slowly.
The completely bounded norm
For  , we write
, we write 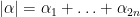 . Any form
. Any form  of degree
of degree 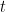 can be written as
can be written as
 ,
,
where  are real coefficients. The first step towards the completely bounded norm of a form is to define the completely bounded norm of a tensor, and the tensor we use is the symmetric
are real coefficients. The first step towards the completely bounded norm of a form is to define the completely bounded norm of a tensor, and the tensor we use is the symmetric 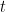 -tensor
-tensor 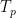 defined as
defined as

where 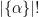 denotes the number of distinct elements in the set formed by the coordinates of
denotes the number of distinct elements in the set formed by the coordinates of 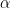 .
.
The relevant norm of 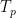 is given in terms of an infimum over decompositions of the form
is given in terms of an infimum over decompositions of the form  , where
, where 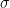 is a permutation of the set
is a permutation of the set  and
and 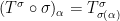 is the permuted element of the multilinear form
is the permuted element of the multilinear form 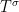 . So that the completely bounded norm of
. So that the completely bounded norm of  is kind of transferred to
is kind of transferred to 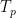 via the definition
via the definition
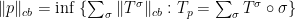 .
.
Just to recap, with the coefficients of the polynomial  we define the symmetric
we define the symmetric 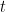 -tensor
-tensor 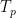 , which is then decomposed into the sum of permuted tensor (multilinear form)
, which is then decomposed into the sum of permuted tensor (multilinear form) 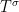 . We then define the completely bounded norm of
. We then define the completely bounded norm of  as the infimum of the sum of the completely bounded norm of such tensor, but now without permuting it. Of course, we haven’t yet defined the completely bounded norm of such tensor, that is, what is
as the infimum of the sum of the completely bounded norm of such tensor, but now without permuting it. Of course, we haven’t yet defined the completely bounded norm of such tensor, that is, what is 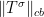 ? We will explain it now.
? We will explain it now.
The idea is to get a bunch of collections of 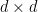 unitary matrices
unitary matrices 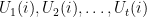 for
for 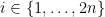 and consider the quantity
and consider the quantity
 .
.
We multiply the unitaries from these collections and sum them using the tensor 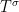 as weight, and then take the norm of the resulting quantity. But here we are using a different norm, the usual operator norm defined for a given operator
as weight, and then take the norm of the resulting quantity. But here we are using a different norm, the usual operator norm defined for a given operator 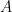 as
as 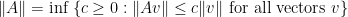 . Finally, with these ingredients in hand, we can define the completely bounded norm for
. Finally, with these ingredients in hand, we can define the completely bounded norm for 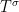 , which is just the supremum over the positive integer
, which is just the supremum over the positive integer  and the unitary matrices, that is,
and the unitary matrices, that is,
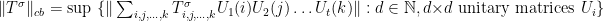 .
.
If we can obtain the supremum of such norm over the size of the unitary matrices and the unitary matrices themselves, then we obtain the completely bounded norm of the tensor 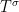 , and from this we get the completely bounded norm of the associated form
, and from this we get the completely bounded norm of the associated form  . Is there such a degree-
. Is there such a degree-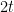 form with
form with 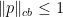 that approximates the function
that approximates the function 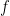 we want to solve? If yes, then there is a
we want to solve? If yes, then there is a 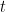 -query quantum algorithm that solves
-query quantum algorithm that solves 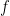 .
.
The proof
Let us briefly explain the proof of the quantum algorithms characterization that we stated above. Their proof involves three main ingredients. The first one is a theorem by Christensen and Sinclair showing that the completely-boundedness of a multilinear form is equivalent to a nice decomposition of such multilinear form. In other words, for a multilinear form  , we have that
, we have that  if and only if we can write
if and only if we can write  as
as
 , (1)
, (1)
where 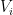 are contractions (
are contractions ( for every
for every  ) and
) and 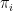 are *-representations (linear maps that preserve multiplication operations,
are *-representations (linear maps that preserve multiplication operations, 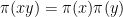 ).
).
The second ingredient gives an upper bound on the completely bounded norm of a certain linear map if it has a specific form. More specifically, if 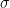 is a linear map such that
is a linear map such that 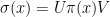 , where
, where 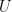 and
and 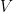 are also linear maps and
are also linear maps and 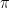 is a *-representation, then
is a *-representation, then  .
.
The third ingredient is the famous Fundamental Factorization Theorem that “factorizes” a linear map in terms of other linear maps if its completely bounded norm is upper bounded by these linear maps. In other words, if 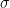 is a linear map and exists other linear maps
is a linear map and exists other linear maps 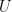 and
and 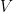 such that
such that 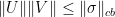 , then, for every matrix
, then, for every matrix 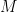 , we have
, we have 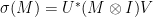 .
.
With these ingredients, they proved an alternative decomposition of equation (1) which was later used to come up with a quantum circuit implementing the tensor 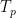 and using
and using 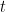 queries, and then showed that this tensor
queries, and then showed that this tensor 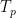 matched the initial form
matched the initial form  . This alternative decomposition is
. This alternative decomposition is
 , (2)
, (2)
where 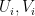 are contractions,
are contractions, 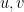 are unit vectors,
are unit vectors, 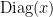 is the diagonal matrix whose diagonal forms
is the diagonal matrix whose diagonal forms  . The above decomposition is valid if, similarly to (1),
. The above decomposition is valid if, similarly to (1),  .
.
We can see that the decomposition involves the operator 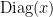 intercalated by unitaries
intercalated by unitaries 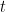 times. Having
times. Having 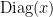 as the query operator, it is possible then to come up with a quantum circuit implementing the decomposition (2). If we look more closely, decomposition (2) has unit vectors on both the left and right sides, which looks like an expectation value. So what is going on is that decomposition (2) can be used to construct a quantum circuit whose expectation value matches
as the query operator, it is possible then to come up with a quantum circuit implementing the decomposition (2). If we look more closely, decomposition (2) has unit vectors on both the left and right sides, which looks like an expectation value. So what is going on is that decomposition (2) can be used to construct a quantum circuit whose expectation value matches 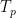 , and hence the polynomial
, and hence the polynomial  used to construct
used to construct 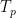 . We won’t get into much details, but we will leave the quantum circuit so that the reader can have a glimpse of what is going on.
. We won’t get into much details, but we will leave the quantum circuit so that the reader can have a glimpse of what is going on.

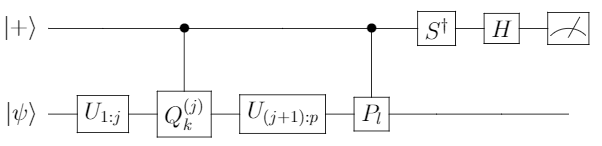
In the above figure representing a quantum circuit that has 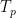 as its expectation value, the registers C, Q, W denote control, query and workspace registers. The unitaries
as its expectation value, the registers C, Q, W denote control, query and workspace registers. The unitaries  are defined by
are defined by 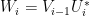 , the unitaries
, the unitaries  have
have  and
and 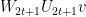 as their first rows, where
as their first rows, where 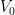 and
and  are isometries (
are isometries (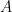 is an isometry iff
is an isometry iff 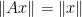 for every
for every  ).
).
Application of the characterization: separation for quartic polynomials
A couple of years ago, in 2016, Aaronson et al. showed that the bounded norm (and also the completely bounded norm that we spent some time describing) is sufficient to characterize quadratic polynomials. More specifically, they showed that for every bounded quadratic polynomial  , there exists a one-query quantum algorithm that returns a random sign with expectation
, there exists a one-query quantum algorithm that returns a random sign with expectation  on input
on input  , where
, where 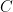 is an absolute constant. This readily prompted the question of whether the same is valid for higher-degree polynomials, that is, if the bounded norm suffices to characterize quantum query algorithms.
is an absolute constant. This readily prompted the question of whether the same is valid for higher-degree polynomials, that is, if the bounded norm suffices to characterize quantum query algorithms.
As you might expect by now, the answer is no, since it is the completely bounded norm that suffices, and Arunachalam et al. used their characterization to give a counterexample for bounded quartic polynomials. What they showed is the existence of a bounded (not completely bounded) quartic polynomial p that for any two-query quantum algorithm whose expectation value is  , one must have
, one must have  , thus showing that
, thus showing that 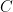 is not an absolute constant. The way they showed this is by using a random cubic form that is bounded, but whose completely bounded norm is
is not an absolute constant. The way they showed this is by using a random cubic form that is bounded, but whose completely bounded norm is  and then embedded this form into a quartic form.
and then embedded this form into a quartic form.
Conclusions
The characterization they found is, in my opinion, apart from the obvious point that it answers the open question of the converse of the polynomial method, quite interesting in the sense that the set of polynomials we should look at is the ones that are bounded by a particular norm, the completely bounded norm. The interesting point is exactly this one, the connection between quantum query algorithms and the completely bounded norm that was first introduced in the general context of tensor products of operator spaces as mentioned before. The norm itself looks quite exotic and complicated, which is linked to a question that Scott Aaronson made at the end of Arunachalam’s talk in QIP 2019, “sure, we could define a particular norm as one that restricts the set of polynomials to the ones that admit a converse to the polynomial method”. Of course, such a norm would not be quite an interesting one. He carries on with something like “In what is this completely bounded norm different compared to that?”. If I remember correctly, Arunachalam gave an answer on the lines of the completely bounded norm appearing in a completely different context. But I still find it surprising that you would go through all the exotic definitions we mentioned above for the completely bounded norm and discover that it is what is needed for the converse of the polynomial method.