Chris Cade – Bristol Quantum Information Theory

There were a few great talks in the ‘query complexity session’ of QIP this year: including Srinivasan Arunachalam’s talk “A converse to the polynomial method” (joint work with Briët and Palazuelos – see João’s post below for a discussion of this) and André Chailloux’s talk entitled “A note on the quantum query complexity of permutation symmetric functions”. In this post I’ll discuss the talk/paper “A Quantum Query Complexity Trichotomy for Regular Languages“, which is the work of Scott Aaronson, Daniel Grier (who gave the talk), and Luke Schaeffer.

Anybody who took courses on theoretical computer science will probably, at some point, have come across regular languages and their more powerful friends. They might even remember their organisation into Chomsky’s hierarchy (see Figure 1). Roughly speaking, a (formal) language consists of an alphabet of letters, and a set of rules for generating words from those letters. With more complicated rules come more expressive languages, for which the sets of words that can be generated from a given alphabet becomes larger. Intuitively, the languages in Chomsky’s hierarchy become more expressive (i.e. larger) as we move upwards and outwards in Figure 1.

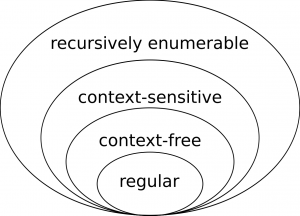
Figure 1: Chomsky’s hierarchy. Technically, the hierarchy contains formal grammars, where these grammars generate the corresponding formal languages.

One might view this hierarchy as an early attempt at computational complexity theory, where we are trying to answer the question “Given more complex rules (e.g. more powerful computational models), what kinds of languages can we generate?”. Indeed, modern computational complexity theory is still defined in terms of languages: complexity classes are defined as the sets of the formal languages that can be parsed by machines with certain computational powers.

However, there have been surprisingly few attempts to study the relationships between modern computational complexity and the kinds of formal languages discussed above. The recent work by Scott Aaronson, Daniel Grier, and Luke Shaeffer on the quantum query complexity of regular languages takes a (large) step in this direction.

This work connects formal language theory to one of the great pillars of modern computational complexity – query complexity. Also known as the ‘black box model’, in this setting we only count the number of times that we need to query (i.e. access) the input in order to carry out our computation. For many problems, the query complexity just ends up corresponding to the number of bits of the input that need to be looked at in order to compute some function.

Why do we study query complexity? The best answer is probably that it allows us prove lower bounds – in contrast to the plethora of conjectures and implications that permeate the circuit complexity world, it is possible to actually prove concrete query lower bounds for many problems, which, in turn, imply rigorous separations between various models of computation. For instance, the study of quantum query complexity led to the proof of optimality of Grover’s algorithm, which gives a provable quadratic separation between classical and quantum computation for the unstructured search problem.

In what follows, we can consider the query complexity of a regular language to correspond to the number of symbols of an input string $x$ that must be looked at in order to decide if $x$ belongs to a given regular language. Here, a language is some (not necessarily finite) set of words that can be built from some alphabet of letters according to a set of rules. By changing the rules, we obtain a different language.

We’ll start with some background on regular languages, and then discuss the results of the paper and the small amount of previous work that has investigated similar connections.

Background: Regular languages

Formally, a regular language over an alphabet $\Sigma$ is any language that can be constructed from:

The empty language $\varnothing$ .
The empty string language $\{\epsilon\}$ .
The `singleton’ languages $\{a\}$ consisting of a single letter $a \in \Sigma$ from the alphabet.
Any combination of the operators
- Concatenation ( $AB$ ): ‘ $A$ followed by $B$ ‘.
- Union ( $A \cup B$ ): ‘either $A$ or $B$ ‘.
- The Kleene star operation ( $A^*$ ): ‘zero or more repetitions of $A$ ‘.

Readers with some coding experience will probably have encountered regular expressions. These are essentially explicit expressions for how to construct a regular language, where we usually write $|$ for union and omit some brackets. For example, to construct a regular language that recognises all words (over the Roman alphabet) that begin with ‘q’ and end with either ‘tum’ or ‘ta’, we could write the regular expression $q\Sigma^*(tum|ta)$ . In this case, the words ‘quantum’ and ‘quanta’ are contained in the regular language, but the words ‘classical’ and ‘quant’ are not. A more computationally motivated example is the regular expression for the $\mathsf{OR}$ function over the binary alphabet $\Sigma = \{0,1\}$ , which we can write as $\Sigma^*1\Sigma^*$ (i.e. ‘a 1 surrounded by any number of any other characters’).

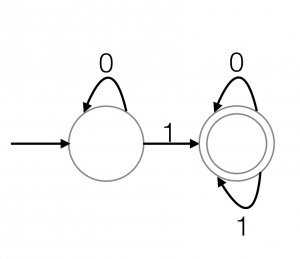
There are many other equivalent definitions of the regular languages. A particularly nice one is: “The set of languages accepted by deterministic finite state automata (DFAs)”. Here, we can roughly think of a (deterministic) finite state automaton as a ‘Turing machine without a memory tape’, which are usually drawn diagrammatically, as in Figure 2. Other definitions include those in terms of grammars (e.g. regular expressions, prefix grammars), or algebraic structures (e.g. recognition via monoids, rational series).

The decision problem associated with a regular language is: Given some string $x$ and a language $L$ , is $x$ in $L$ ? Often, we want to make this decision by reading in as few bits of $x$ as possible (hence the motivation to study the query complexity of regular languages).

Figure 2: DFA for the OR function. Each circle represents a ‘state’ of the machine, each arrow is a transition from one state to another, conditioned on taking as input a letter from the alphabet. The double-lined state (circle on the right) represents an ‘accepting’ state.

Main results

The main result of the paper by Aaronson et al. is a trichotomy theorem, stated informally as follows:

Every regular language has quantum query complexity $\Theta(1), \tilde{\Theta}(\sqrt{n})$ , or $\Theta(n)$ . Furthermore, each query upper bound results from an explicit quantum algorithm.

The authors arrive at this result by showing that all regular languages naturally fall into 1 of 3 categories:

‘Trivial’ languages: Intuitively, these are the languages for which membership can be decided by the first and last characters of the input string. For instance, the language describing all binary representations of even numbers is a trivial language.
Star-free languages: The variant of regular languages where complement is allowed ( $\overline A$ — i.e. `something not in $A$ ‘), but the Kleene star is not. Note that these languages can still be infinite — indeed, the language $\overline\varnothing$ is equivalent to the language $\Sigma^*$ . The quantum query complexity of these languages is $\tilde{\Theta}(\sqrt{n})$ .
All the rest, which have quantum query complexity $\Theta(n)$ .

The paper mostly describes these classes in terms of the algebraic definitions of regular languages (i.e. in terms of monoids), since these form the basis of many of the results, but for the sake of simplicity, we will avoid talking about monoids in this post.

Along the way, the authors prove several more interesting results:

Algebraic characterisation: They give a characterisation of each class of regular languages in terms of the monoids that recognise them. That is, the monoid is either a rectangular band, aperiodic, or finite. In particular, given a description of the machine, grammar, etc. generating the language, it is possible to decide its membership in one of the three classes mentioned above by explicitly calculating its ‘syntactic monoid’ and checking a small number of conditions. See Section 3 of their paper for details.
Related complexity measures: Many of the lower bounds are derived from lower bounds on other query measures. They prove query dichotomies for deterministic complexity, randomised query complexity, sensitivity, block sensitivity, and certificate complexity: they are all either $\Theta(1)$ or $\Theta(n)$ for regular languages. See Section 6 of their paper.
Generalisation of Grover’s algorithm: The quantum algorithm using $\tilde{O}(\sqrt{n})$ queries for star-free regular languages extends to a variety of other settings by virtue of the fact that the star-free languages enjoy a number of equivalent characterisations. In particular, the characterisation of star-free languages as sentences in first-order logic over the natural numbers with the less-than relation shows that the algorithm for star-free languages is a nice generalisation of Grover’s algorithm. See Sections 1.3 and 4 of their paper for extra details and applications.

Finally, the authors show that the trichotomy breaks down for other formal languages. In fact, it breaks down as soon as we move to the ‘next level’ of the hierarchy, namely the context-free languages.

The results in the paper allow the authors to link the query complexities to the more familiar (for some) setting of circuit complexity. By the characterisation of star-free languages in first-order logic (in particular, McNaughton’s characterisation of star-free languages in first-order logic, which says that every star-free language can be expressed as a sentence in first-order logic over the natural numbers with the less-than relation and predicates $\pi_a$ for $a \in \Sigma$ , such that $\pi_a(i)$ is true if input symbol $x_i$ is $a$ .), it follows that all star-free languages that have quantum query complexity $\tilde{O}(\sqrt{n})$ are in $\mathsf{AC^0}$ . Conversely, they show that regular languages not in $\mathsf{AC^0}$ have quantum query complexity $\Omega(n)$ . Thus, another way to state the trichotomy is that (very roughly speaking) regular languages in $\mathsf{NC^0}$ have complexity $O(1)$ , regular languages in $\mathsf{AC^0}$ but not $\mathsf{NC^0}$ have complexity $\tilde{\Theta}(\sqrt{n})$ , and everything else has complexity $\Omega(n)$ .

Previous work

There have been other attempts to connect the more modern aspects of complexity theory to regular languages, as the authors of this work point out. One example is the work of Tesson and Thérien on the communication complexity of regular languages. They show that the communication complexity is $\Theta(1)$ , $\Theta(\log \log n)$ , $\Theta(\log n)$ , or $\Theta(n)$ — a `tetrachotomy’ theorem with parallels to the current work. It is interesting that Tesson and Thérien didn’t study the query complexity of regular languages, and instead went straight for the communication complexity setting, since the former is the more obvious first step. Indeed, Aaronson et al. write

“communication complexity is traditionally more difficult than query complexity, yet the authors appear to have skipped over query complexity — we assume because quantum query complexity is necessary to get an interesting result.”

Another example of previous work is the work of Alon, Krivelevich, Newman, and Szegedy, who consider regular languages in the property-testing framework. Here the task is to decide if an $n$ -letter input word $x$ is in a given language, or if at least $\epsilon n$ many positions of $x$ must be changed in order to create a word that is in the language. They show that regular languages can be tested, in this sense, using only $\tilde{O}(1/\epsilon)$ queries. They also demonstrate that there exist context-free grammars which do not admit constant query property testers – showing that the results once again break down once we leave the regular languages.

Aaronson et al. also point out some similarities to work of Childs and Kothari on the complexity of deciding minor-closed graph properties (the results are of the same flavour, but not obviously related), and that a combination of two existing results – Chandra, Fortune, and Lipton and Bun, Kothari, and Thaler – allows one to show that the quantum query complexity of star-free languages is $o(n)$ .

Techniques

The lower bounds are mostly derived from a (new) dichotomy theorem for sensitivity – i.e. that the sensitivity of a regular language is either $O(1)$ or $\Omega(n)$ . The proof makes a nice use of the pumping lemma for regular languages.

The majority of the work for the rest of the paper is focused on developing the quantum query algorithm for star-free languages. The proof is based on an algebraic characterisation of star-free regular languages as ‘those languages recognised by finite aperiodic monoids’, due to Schützenberger, and the actual algorithm can be seen as a generalisation of Grover’s algorithm. I’ll leave the exact details to the paper.

These two short paragraphs really don’t do justice to the number of different techniques that the paper combines to obtain its results. So I recommend checking out the paper for details!

Summary and open questions

This work takes a complete first step towards studying formal languages from the perspective of the more modern forms of computational complexity, namely query complexity. It very satisfyingly answers the question “what is the query complexity of the regular languages?”. For classical computers, it’s either $\Theta(1)$ or $\Theta(n)$ – i.e. either trivial or difficult. For quantum computers, it’s either $\Theta(1)$ , $\Theta(n)$ , or $\tilde{\Theta}(\sqrt{n})$ – i.e. trivial, difficult, or slightly easier than classical.

An obvious next step is to extend this work to other languages in the hierarchy, for example the context-free languages. However, the authors obtain what is essentially a no-go result in this direction – they show that the trichotomy breaks down, and in particular for every $c \in [1/2, 1]$ , there exists some context-free language with quantum query complexity approaching $\Theta(n^c)$ . They conjecture that no context-free language will have quantum query complexity that lies strictly between constant or $\sqrt{n}$ , but leave this open.

Another direction is to consider promise problems: suppose we are promised that the input strings are taken from some specific set, does this affect the query complexity? It is known that in order to obtain exponential separations between classical and quantum query complexity for (say) Boolean functions, we have to consider partial functions – i.e. functions with a promise on the input. For instance, suppose we are promised that the input is ‘sorted’ (i.e. belongs to the regular language generated by $0^*1^*$ ). Then our task is to determine whether there is an occurrence of $01$ at an even position (belongs to the language $(\Sigma\Sigma)^*01\Sigma^*$ ). As the authors point out, we can use binary search to decide membership in only $\Theta(\log n)$ quantum (and classical) queries, so clearly complexities other than the three above are possible. Aaronson et al. conjecture that the trichotomy would remain, though, and that the quantum query complexity of regular languages with promises on their inputs is one of $\Theta(\text{polylog}(n))$ , $\Theta(\sqrt{n}\cdot\text{polylog}(n))$ , or $\Theta(n\cdot\text{polylog}(n))$ .

It’d also be nice to see if there are any other applications of the Grover-esque algorithm that the authors develop. Given that the algorithm is quite general, and that there are many alternative characterisations of the star-free regular languages, it’d be surprising if there weren’t any immediate applications to other problems. The authors suggest that string matching problems could be an appropriate setting, since linear-time classical algorithms for these problems have been derived from finite automata. Although quadratic quantum speedups are already known here, it could be a good first step to obtain these speedups by just applying the new algorithm as a black box.

Author: Chris Cade

A Quantum Query Complexity Trichotomy for Regular Languages (Aaronson, Grier, and Shaeffer 2018)

Background: Regular languages

Main results

Previous work

Techniques

Summary and open questions